We now have as a primitive operation that the Fourier transform
is a fast process on a
quantum computer. Note that while the Fast Fourier transform on a conventional
computer takes of order ![]() steps, on a quantum computer the Fast Fourier
transform of the state (note this is of the state, not of a collection of
steps, on a quantum computer the Fast Fourier
transform of the state (note this is of the state, not of a collection of ![]() input numbers) takes only of order
input numbers) takes only of order ![]() steps.
steps.
The first really significant result of Quantum Computing was Peter Shor's demonstration that factoring could be fast on a quantum computer. He accompished this by noticing that if one could find the period of a certain periodic function depending on the number in questin, one could factor that number. Finding that period made use of the quantum Fourier transform. In order to see how, we need to look at some number theory.
Let us assume that we have some integer ![]() , which is the product of two prime
factors
, which is the product of two prime
factors ![]() and
and ![]() . There are then a number of features of numbers which are
important.
. There are then a number of features of numbers which are
important.
Definition: mod operation. Given two integers, ![]() and
and ![]() , the term
, the term ![]() means that integer, between
means that integer, between ![]() and
and ![]() which is the remainder when you
divide
which is the remainder when you
divide ![]() by
by ![]() . I.e.,
. I.e.,
![]() for some integer
for some integer ![]() .
.
Now, for some number ![]() lying between 1 and
lying between 1 and ![]() , which shares no common
factors with
, which shares no common
factors with ![]() ,
consider
,
consider ![]() .
Eventually for some (smallest) value of
.
Eventually for some (smallest) value of ![]() , this must be equal to
, this must be equal to ![]() .
( since there are only
.
( since there are only ![]() possible numbers that this could be, eventually one power must equal some other
power. I.e.,
possible numbers that this could be, eventually one power must equal some other
power. I.e.,
![]() which means that
which means that ![]() divides
divides
![]() . Since x has no common factors with
. Since x has no common factors with ![]() , neither does
, neither does
![]() , so
, so ![]() must be a multiple of
must be a multiple of ![]() and
and
![]() .
Define
.
Define ![]() as the smallest such power.
as the smallest such power.
Then the function ![]() is a periodic function in
is a periodic function in ![]() with period
with period ![]() .
There are now three possibilities for that
.
There are now three possibilities for that ![]() :
:
a)![]() is odd;
is odd;
If ![]() is even then we can write
is even then we can write ![]() , which is a multiple of
, which is a multiple of ![]() as
as
![]() . Then, either
. Then, either
b) ![]() divides
divides
![]() , in which case our
, in which case our
![]() was not the smallest possible value of
was not the smallest possible value of ![]() ,
,
c) ![]() divides
divides
![]() ,
,
or
d) or one, but not both, of
the factors of ![]() divides
divides
![]() ( and thus also
( and thus also
![]() .) I.e.,
.) I.e., ![]() and
and
![]() have a common factor.
have a common factor.
If two numbers have a common factor, one can rapidly discover what that common
factor is using Euclid's algorithm. If two numbers have a common factor, then
the remainder when dividing the
larger by the smaller also has the same common factor. Successively dividing in
this way eventually leads to that unique greatest common factor in a time less
than of
order ![]() .
.
Thus, if we can find the period of the function ![]() ,
we can test whether this
,
we can test whether this ![]() falls into category d, and if it does, we have a
factor of
falls into category d, and if it does, we have a
factor of ![]() . If it does not, (i.e.,
. If it does not, (i.e., ![]() falls
under classes a,b, or c), we try with another value of
falls
under classes a,b, or c), we try with another value of ![]() . For randomly
selected x, Shor claimed that there will be at least a 50% probability
that the
. For randomly
selected x, Shor claimed that there will be at least a 50% probability
that the ![]() will fall into
class d, and that we will have a solution. After testing a small number of
randomly chosen
will fall into
class d, and that we will have a solution. After testing a small number of
randomly chosen ![]() , the probability will become overwhelming
that we will have found the factor.
Note that the Shor algorithm is not a deterministic one. It is one in which the
probability of not finding the right answer decreases at least exponentially
with the number of trials.
, the probability will become overwhelming
that we will have found the factor.
Note that the Shor algorithm is not a deterministic one. It is one in which the
probability of not finding the right answer decreases at least exponentially
with the number of trials.
The solution thus hinges on finding the period of the
function, ![]() for a given
for a given ![]() . Finding periods is ideally
suited to a Fourier
Transform. To do this, first design a computer which
takes a state
. Finding periods is ideally
suited to a Fourier
Transform. To do this, first design a computer which
takes a state ![]() and calculates
and calculates
![]() .
This need not even be a
reversible computer as long as nothing in the environment becomes correlated
with
.
This need not even be a
reversible computer as long as nothing in the environment becomes correlated
with ![]() . This can be done
in a number of operations of order
. This can be done
in a number of operations of order ![]() where
where ![]() is a number like
3. Then feed into this computer the state
is a number like
3. Then feed into this computer the state
![]() , where
, where ![]() is the first integer larger than
is the first integer larger than ![]() -- i.e.,
-- i.e., ![]() .
The maximum value of
.
The maximum value of ![]() is thus greater than
is thus greater than ![]() .
This will produce the state
.
This will produce the state
![]() . Measure the
output state, (the bits which
correspond to the output,
. Measure the
output state, (the bits which
correspond to the output, ![]() but not the input state. Assume
that this measurement gave the value
but not the input state. Assume
that this measurement gave the value ![]() (it does not matter what this value
actually is. It plays no role. This measurement need not even be carried out at
this point, since those output bits will play no further role in the calculation
and could also be measured a the end of the experiment). This
will leave the system in the state
(it does not matter what this value
actually is. It plays no role. This measurement need not even be carried out at
this point, since those output bits will play no further role in the calculation
and could also be measured a the end of the experiment). This
will leave the system in the state
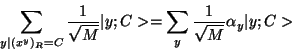 |
(15) |
We have a state in which the amplitudes are periodic and can do a Fourier
transform of these amplitudes. The resultant state will be
![]() , where the
, where the
![]() are the Fourier transform of the
are the Fourier transform of the
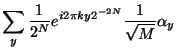 |
|||
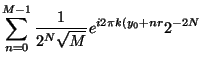 |
|||
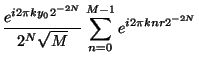 |
(16) |
| (17) |
| (18) |
A measurement of ![]() will then give a us a number which is a multiple of
will then give a us a number which is a multiple of
![]() .
Unless
.
Unless ![]() and the multiple have a common factors (a rare situation),
one can uniquely determine
and the multiple have a common factors (a rare situation),
one can uniquely determine ![]() from the measured value of
from the measured value of ![]() .
One can then use that
.
One can then use that ![]() to
try to find the common factors of
to
try to find the common factors of ![]() and
and ![]() . If one finds a common
factor, one has a factor of
. If one finds a common
factor, one has a factor of ![]() . If one does not, one tries again with a
different value of
. If one does not, one tries again with a
different value of ![]() . The probability is thus very high that in only a few
attempts one will have found a factors
. The probability is thus very high that in only a few
attempts one will have found a factors ![]() .
.