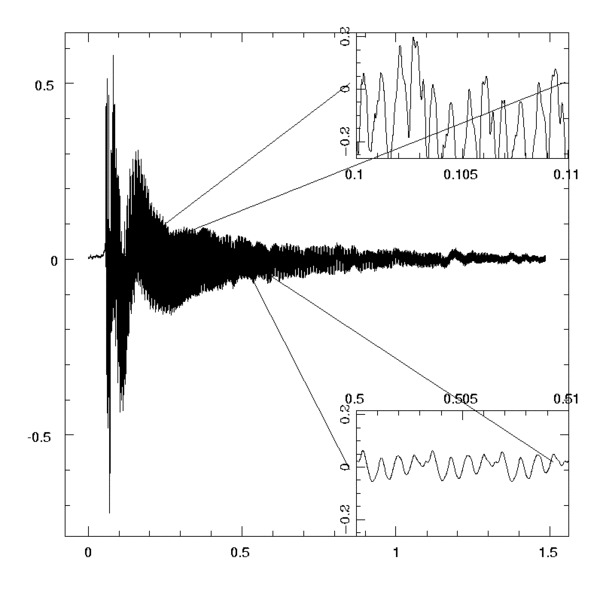
If you click on the image, you can hear what this guitar pluck sounds like

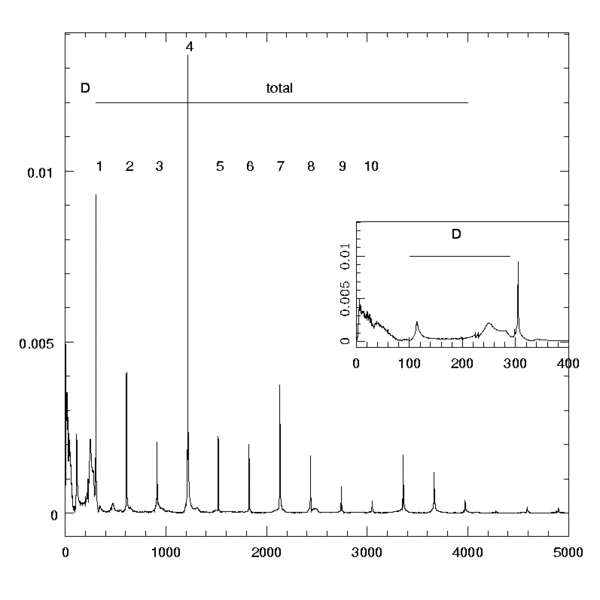
Here we look at the spectrum of the above guitar pluck. We clearly see the fundamental and its harmonics sharply plotted at integer multiples of approximately 300 Hz. If you click on each number of the harmoic, you can hear what that harmonic (that mode of the string) sounds like separated out from the rest of the sounds. Note that the second is an octave higher, the third and octave and a perfect fifth, the fourth is two octaves, the fifth, two octaves and a major third, the sixth is two octaves and a fifth, the seventh-- well it is not really near any interval. The eights is two octaves, the nineth is two octaves and a whole tone, etc.
Again if you click on the numbers, you can hear that mode play. If you click on the word "total", you will hear the totalled sound of the first 14 harmonics. Note that this is a good approximation to the sound of the guitar pluck, except for the very beginning, where it starts too smoothly. If you click on the D either at the left of the main graph or in the insert, you will hear the guitar pluck with those fourteen harmonics cancelled out. The sound is very brief, and percussive. Looking at the fourier transform graph, this sound comes primarily from the two broad an-harmonic broad peaks at about 250Hs and 120Hz. Look especially at the insert in which the range from 0 to 400 Hz in the spectrum is plotted. That second (lower frequency) broad peak is the sound of the fundamental air resonance of the enclosed air withing the guitar, oscillating like a coke bottle with the slug of air in the hole in the top of the guitar the moving mass, and the air in the body the "spring". The higher frequency peak is the sound of the first "drum" mode of the wooden top of the guitar. Both are broad peaks which indicates a low Q, and rapid damping. This "drum-like" sound at the very beginning of the pluck is part of what gives a guitar its distinctive character. It is not a tuned sound-- it lasts too brief a time for the ear to be able to pitch the sound.
This page and all links therefrom are copyright W. G. Unruh. They may be reproduced for non-commercial purposes but this notice must be retained in any copy. Any changes must be clearly indicated as such.
The .wav files and image files were created under MandrakeLinux using SuperMongo, sox, and audacity for recording and manipulating the sound files, and Supermogo and gimp for the graphs.