This is an HTML5 page with .wav sound. If on clicking on the bottom graphs you hear no sound, use this old version
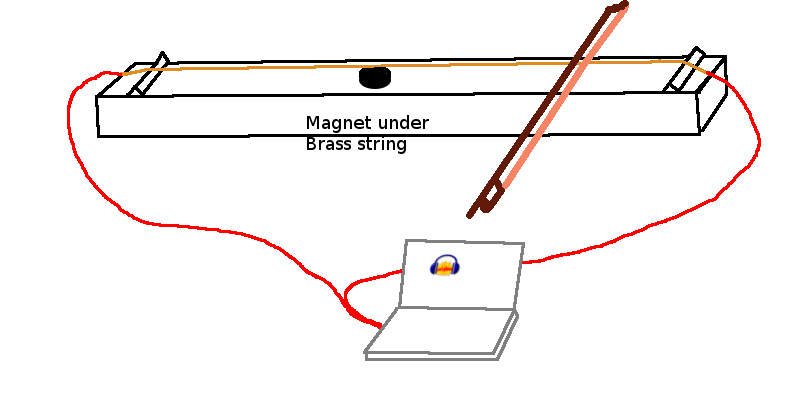
Here are some detailed graphs of the recordings of notes from a bowed monocord with a magnet under the brass string to induce a voltage in the string proportional to the velocity of the string at the point just above the magnet.

There are plots for the magnet placed right under the bow, placed at approximately the midpoint of the string, and near the end furthest from the bowed point. Immediately under the bow, the "stick" period ( while the string approximately sticks to the bow) does not have exactly the velocity of the bow, but gradually decreases, and one might expect because of the increased tension on the string pulling back on the string. The change is small. When the string slips, the slip velocity is also not constant. Note that the time during which the string "sticks", and the string has the low velocity of the bow, is much longer than the time during which the string slips. The string is not exactly "stuck" to the bow, but gradually creeps backward a bit during the stick time. During the slip, note that he velocity is not constant, but is damped as the time goes on, as one would expect since friction of the rosin is not zero even when the velocity is high.
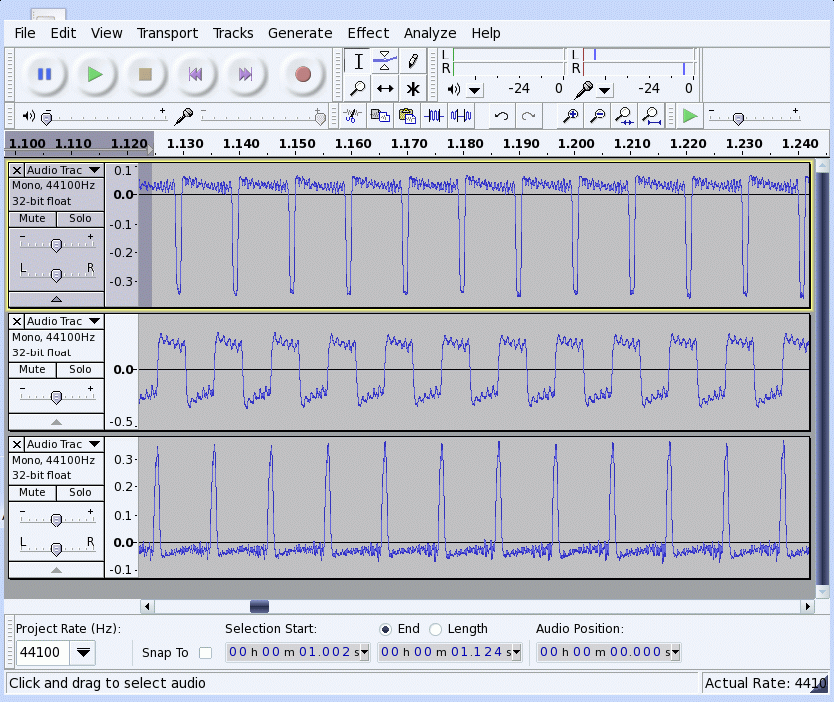
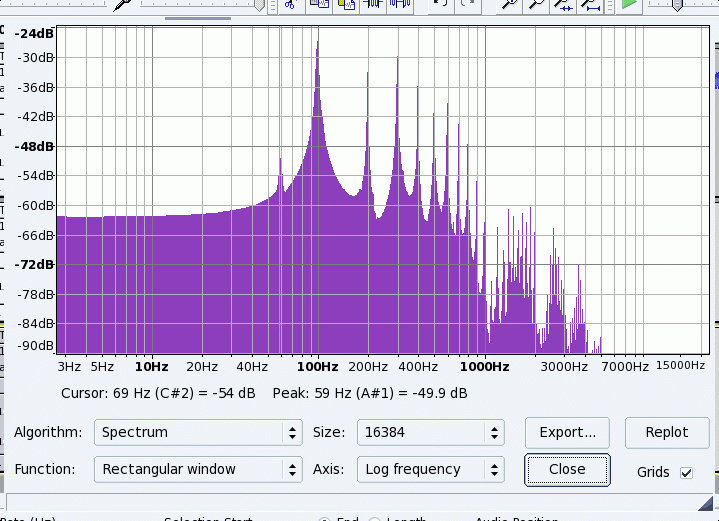
These are the Spectra of those same three velocities of the different positions under the bowed note. The first is the specturm of the velocity at the bowed position.
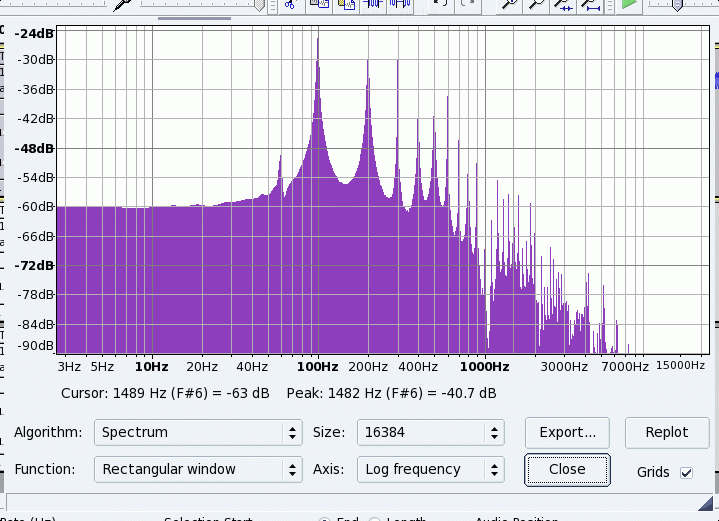
Note that the 10th mode is much less than the other modes near it. The magnet was placed at a point 1/10 of the way from the end of the string-- ie the node to the 10th mode, and one would not expect it to vibrate there.
The small peak at 60Hz is due to "hum" from the 60Hz power lines creating a voltage in the input wires to the amplifier.
Placing the magnet under the middle of the string, we see that the velocity there is approximately a square wave ( with slopes to the velocity) and the spectrum contains less of the higher frequencies than just under the bow. This might be expected, since near the end of the string is much nearer a node for the low numbered modes, than it is for the higher numbered modes.
Also since the even numbered modes all have nodes in the velocity at the center of the string, those nodes should not show up in the spectrum taken at the center of the string. The spectum shows that the even number modes are much lower in intensity than the odd numbered ones.
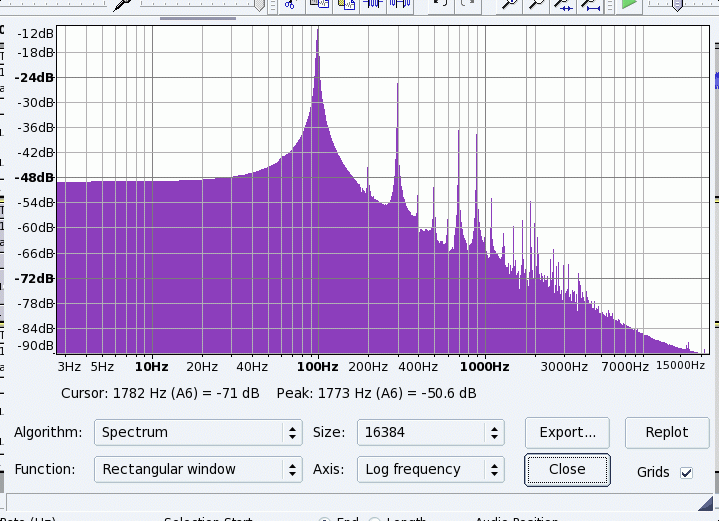
Placing the magnet near the far end of the string at the equivalent position from that end of the string as the bow is from the near end. Note that the velocity is just inverted from that of the bowed end. The slow motion is in the opposite direction to that in which the bow is moving. Note that if you lightly place a non-pulled bow at that point the slow motion of the string will tend to stick to the bow pulling it along with the string, but when the high velocity occurs, the string breaks away from the bow. Ie, that bow tends to move at the same velocity as the bow, but in the opposite direction.
The spectrum is the same as just under bow with very high modes being excitted.
We can hear what the velocity sounds like if that velocity would be the pressure recorded by a microphone (eg if the string were very wide, and the microphone were placed a distance much less than the diameter of the string away from the string.) The sound from the center of the string is almost a square wave, as one would expect from a clarinet, and the sound has the hollow sound of a clarinet. Of course the sound from a string instrument comes from the force exerted on the bridge (roughly the integral of the velocity near the bridge which becomes a saw toothed wave. However, that sound is drastically altered by the resonances of the bridge and of the violin body.
Click on the graph to hear the sound of the velocity at that point.
The .wav files and image files were created under Mandriva Linux using audacity and xv.