
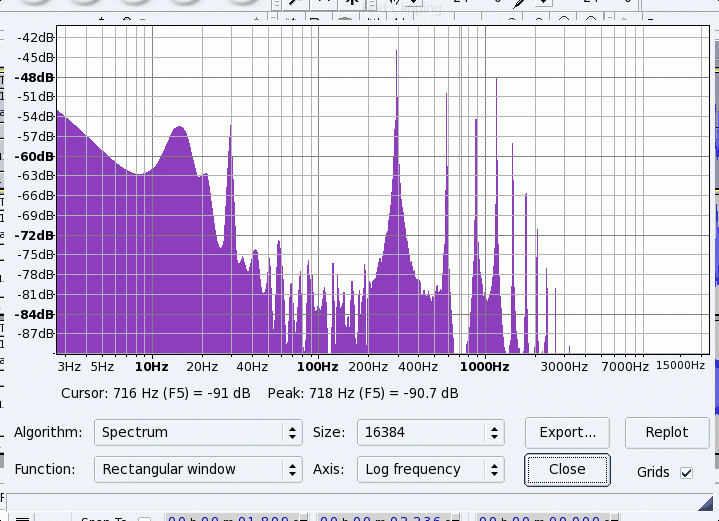
These are the Spectra of those same three notes from the flute, one from the lowest notes on the flute(D4) From both the record of the note itself, and from the spectrum, we would expect the 4th Harminic to be strong (four bumps per period on the recording of the note itself)
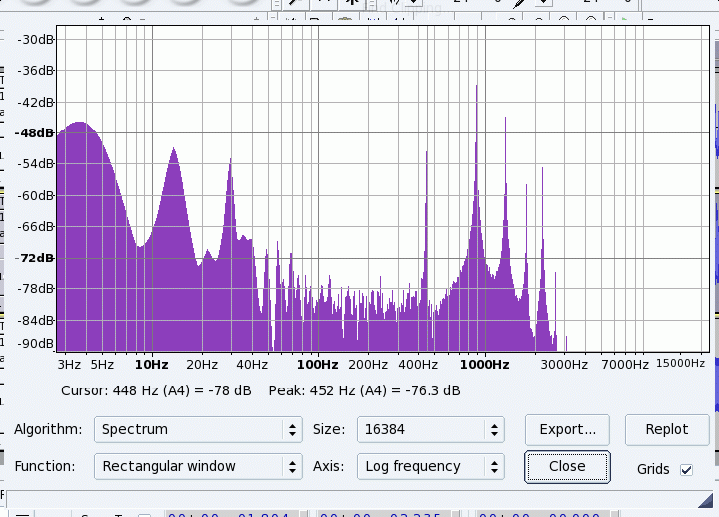
one from the mid (A4) Here we would have expected from the recording of the note that the third harmonic would be strong (three humps per period) and sure enough in the spectrum the third harmonic is strong, even very slightly stronger than the fundamental.
and one from the highest(G6). From the recording we would expect that the fundamental would be strong, and higher harmonics would be much weaker (the bottom-- negative pressures-- are more pointy than the top which suggests that at least some of the higher harmonics are present) The Spectrum confirms this-- the fundamental is far stronger than any of the harmonics, with the second harmonic being the strongest of the upper harmonics.
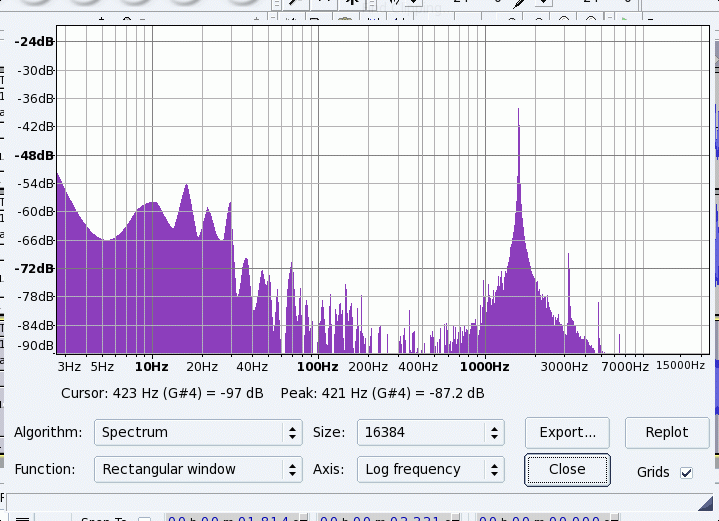
Note that for all of the notes, there is very little energy in harmonics higher than about 3KHz. This is at least in part caused by the short stub in the flute (closed ended pipe) near the mouthpiece. The resonances in this tube tend to cancel out contributions from the rest of the flute in their effect on the amplifier of the stream across the mouthpiece. Again, the junk below about 100 Hz is all noise-- either from the room, or from the electronics in the computer or noise from the computer itself.
The absolute amplitude in dB is simply how far below the loudest sound that the microphone could record without clipping. It is the relative amplitudes of the notes that are important.
As explained in the notes on the Fourier transform in the course notes, the widths of the peaks arise out of the finite time that the note is recorded and the fact that the recording time is not an exact multiple of the period of the note. Both of these effect broaden out the peak.
The number of samples 16384. Since there are 44100 samples per second, this is about .4 seconds. The resolution -- the minimum frequency that can be sample is one whose period is this sample time, so the minimum frequency is about 2.5Hz. The smooth curve at low frequencies is an interpolation by the program and cannot be trusted (eg below about 50Hz)
This page and all links therefrom are copyright W. G. Unruh. They may be reproduced for non-commercial purposes but this notice must be retained in any copy. Any changes must be clearly indicated as such.
The image files were created under Mandriva Linux using audacity and xv.