One off the other things Newton was able to prove was Kepler's second law, or rather to use Kepler's second law to prove that the acceleration of the planets in their orbits always pointed straight to the sun. Ie, it was the center of the sun to which the accelerations of the planets pointed, even if the orbits were not circles.
He showed that if there was a central point toward which the accelerations always pointed then any arbitrary orbit that that acceleration created would be such that it swept out equal areas in equal times. This proof also implied that this would not be true if the accelerations did not all point to that point.

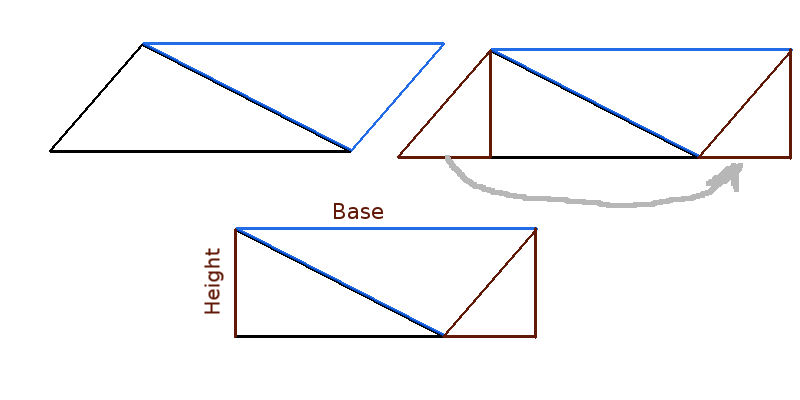
To begin lets remind ourselves of the area of a triangle. The black figure above is the original triangle. Now duplicate it (blue triangle) , rotate by 180 degrees, and adjoin to the original triangle. Now cut perpendicular to the base the left side of the resulting paralellogram (the brown triangle) move it to the right side and adjoin it to the figure. You end up with a rectangle whose area is base times hieght. Ie, the area of the original triangle is half of the base times the perpendicular height to the vertex.

The proof of Kepler's second law has three parts, which are illustrated in the figure. We first consider unaccelerated motion. This would be motion in a straight line with the same distance travelled in the same time along that path. In the figure on the left the black line is the path of the object, and we have that line divided in half which represents the two adjacent parts of the path of the object traversed in equal times. Connect the ends and that central point of the line to some other point (which will eventually be the point to which the acceleration will point). The area of the triangles formed by the two adjacent parts of the path of the particles and the lines connecting them to the central point are given by 1/2 Base times height, where height is the perpendicular height to the base. The height is given by the red line in the first figure. Since the two bases of the triangles are equal, and the height is common and thus the same for the two traingles, the two areas of the two triangles (black-grey triangles) are the same.
Now the formula for the area of a triangle is the same no matter which of the sides of the triangle we choose. Let us now look at the area where we take the common side of the triangle as the common base. The heights will be the distance between the base and the line that goes through the opposite vertex to the base and is parallel to the base (the common base is the blue line, and the parallel lines through the vertices are the two pink lines in the central figure.) the distance between the base and the parallel line is the height, and since we have shown that the two triangles are the same area, the two heights must be the same (since the base is common and thus is the same.
We now use Galileo's combined motion idea. The path along the pink lines marked Height represents the motion of the motion of the particle in the direction perpendicular to the blue line, and the motion along this line is uniform-- equal distances along a straight line in equal times.
We now look at the right figure. In this figure we have left everything the same, except we have had the particle suffer a sudden acceleration at the midpoint. Furthermore, we assume that this acceleration has lasted for an infinitessimal time, and is directed along the line from that midpoint to the "center". By Galileo's combined motion law, the motion in the direction perpendicular to the acceleration remains the same. It was uniform motion without the acceleration, and it is uniform motion with the acceleration. Thus the Heights of the triangles remains the same. The motion parallel to the acceleration of course changes. Thus the distance travelled parallel to the blue line is different before and after the acceleration. But since the Base is the same, and the Heights are the same, the triangles still have the same area. Ie, in equal times the line from the center to the object sweep out equal areas in equal times.
We have shown this for finite times, and sudden acceleations. By taking the times smaller and smaller, making the acceleration smaller and smaller at any one center, and putting in more and more accelerations at successive "midpoints" we have that an an arbitrary central acceleration (Ie, there need be no relation between the central accelerations on each succeeding point) we get that the area swept out by the line joining the object to the fixed center in equal times must always be the same. This is completely independent of the size of the acceleration, only that it always point at the same center. Ie, Kepler's second law is true only if the acceleration of the object always points to the same center.
Thus, going from the first diagram to the second, we simply use geometry as known already by Pythagoras and Euclid at least 500BC. In the second we interpret it as saying that distance travelled by the object in the direction perpendicular to the direction to the center are equal in equal times. Going from the second to the third uses Galileo's composite motion law, that the acceleration does not change the motion perpendicular to the acceleration.
This law became known as the law of the conservation (ie remains the same over time) of angular momentum, and is always true if the acceleration of the object always points to the same central point. Newton used it crucially to argue that this meant that the planets, or the moon, have accelerations caused by the sun, or the earth, which point to the center of the sun or earth. As far as the planets or the moon are concerned it is as if the sun or earth are not extended objects but rather are point like objects all concentrated in some central point, which could only be the "center of mass" as defined by Archimedes.
This is a beautifully simple law, with far reaching consequences.
To show that the inverse square law leads to ellipses is more difficult and I will not go through that proof here, only saying that Newton managed to prove it using geometric arguments like the above. While he (and Hooke, Wren) had used Kepler's third law to derive the inverse square law of accelerations, it was this demonstration which showed that the center of those accelerations must be the sun (for the planets)
Note the crucial role that Kepler and his changes from Ptolemy played in this argument. He transfered the crucial locus of the motion from the Equant point, a point which sits in the void away from the sun, to the sun. Without that change, Newton's task would have been impossible. Ptolemy's uniform rotation around the equant was a wonderful approximation to Kepler's law. It really did fit the observed motion of the planets to an accuracy that was really hard to beat for the naked eye observations available to Ptolemy. It has all of the stucture that Kepler's ellipses had-- a center displaced from the sun and another point, the Equant (the other focus of the ellipse for Kepler). The distortion from the oval shape of the ellipse is also very small. But the crucial action for Ptolomy occured at the Equant, a point sitting off in the void where nothing was located, not at the Sun or earth. Kepler had transfered, by his equal areas in equal times law, the crucial action to the sun or earth allowing recognition by Newton that this implied that the acceleration of all of the planets pointed right toward the sun and of the moon to the earth.
copyright W Unruh (2018)