Since the essence of the world was this sea of particles, he was interested in how they moved and intereacted. How do two bodies behave when they collide? He had no idea of the independence of motion that Galileo had discovered. There was only a single attribute, speed, of motion. One of his conclusions was that if a lighter body hit a heavier body at rest, the light one would simply bounce off, leaving the heavier one stationary (contrary to even the most rudimentary of experiments). In the case of two objects of equal "volume" (the concept of mass, or that the weight of a body denotes some inherent attribute of the body) if they approaced each other with the same speed, they would bounce back with the same speed. If one was at reast and the other hit it with twice some speed, they would bounce with one having 1/2 of that speed, and the other 3/2 of the speed. (any pool player would know differently. If they hit head on, the striking ball would stop and the other would travel with the full incoming speed of the striking ball. Ie, in general his thoughts were in fact far less reliable a guide to the truth than would even the most rudimentary sense perceptions have been. His writing however was so persuasive and forceful that he, at least initially, convinced all that read him. (His philosophy still heavily ifluences French thought. But in one aspect he had an idea that was at least slightly better than Galileo, in that he believed that the natural state of motion of a body was in a straight line, not in a circle around the earth. (Whether this is because he only thought of experiments in the small scale where there would be no difference between the two, or not.) For him the planets moved in their orbits because of vortices sent out by the sun (he did believe in Copernicanism, but stopped publishing when he heard about what had happened to Galileo).
Descarte also worried about what he called centripital force. If you swing a weight around your head, it feels as thought there is a force pulling the weight outward. But again his ideas were confused.
It was Huygens(1629-1695) in Holland, and Paris, who thought much more clearly. Descarte (1596-1650) was 30 years younger than Galileo (1564-1642), but incorporated little of Galileo into his physics. Huygens was strongly influenced by Descarte and Galileo, being convinced by Descarte in his youth, but then revolting against many of his thoughts later. In the case of the motion of bodies, he believed that the natural motion was straight line motion, not circles around the earth. But he took to hearth Galileo's "relativity" ideas. Thus one could use the fact that a traveller could have as valid a viewpoint of the physics as someone at rest. If one were to consider two equal mass balls colliding, then from the viewpoint of an observer at rest, the two balls could be coming straight at each other each with the same velocity. When they collide they would, as Descarte said (and as symmetry would dictate, since there would be nothing to distinguish one ball from the other), they should bounce back with same speed. But now regard the same experiment if you were floating past in a boat.Now with respect to you, one of the balls (the one travelling in the opposite direction to you) would be travelling faster by the speed of the boat, and the one travelling with you would be going more slowly by the speed of the boat. In the collision, the fact that you were observing it from a boat would make no difference to the facts of the collision. They would, in the view of the person on the bank, bounce back with the same speed as they came in, but from the view of the person on the boat, the one that had approached with the speed plus the boat speed would bounce back with the speed minus the boat speed. And the one that had been approaching the collision with the speed minus the boat speed, would bounce back with the speed plus the boat speed. But this should also be true if the original experiment had been done on the boat, and observed from the bank. Ie, one could determine the outcome of the head on collision where the two balls had arbitrary speeds with respect to each other, simply by knwoing what would happen if the collision took place with equal but opposite speeds. Similarly one could determine what would happen with arbitrary directions of the two speeds, by thinking of the boat having arbitrary motions-- ie not necessarly parallel to the directions of the balls.
From his study of Archimedes and when objects were "balanced" he knew of the concept of the "center of mass". This is the point at which if you held the object there, it would be balanced. If would not fall off to one side or the other. For two equal mass and shaped bodies (like the billiard balls) this center of mass lies directly and half way between the two objects. If the two balls were flying directly at each other, this center of mass would be at rest since the point directly between the two balls would be at rest. If the balls were not flying directly toward each other with the same velocity, one could, by the above argument always find a way of moving the boat so that according to the boat, both balls were flying toward each other with the same speed. For the person in the boat the center off mass would be at rest. For the person on the bank therefor the center of mass would be moving with the velocity of boat, which would be the same both before and after the collision. Thus, during and after the collision, the motion of the center of mass would be the same. It would not be affected by the collision.
The center of mass could be simply calculated, and had been done so by Archimedes 2000 years earlier, for even quite complicated shapes. It was the point of balance of the system. It was determined by taking each little piece of mass of the system, multiplying it by the distance from the center, and adding them up. And this distance was the distance separately in the x, the y and the z directions. It thus seemed that in collisions between parts, one of the rules should be that the center of mass should move uniformly before, during and after the collision.
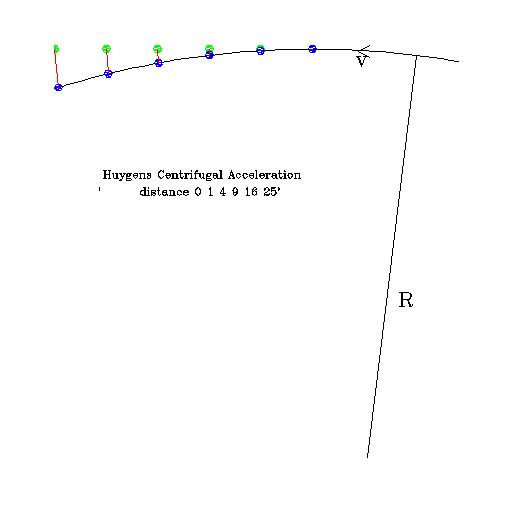
He also thought more about the problem of "centrifugal" force. He knew that if
one released the string holding the ball as it circled around, it would fly
off, in a direction tangent to circle it had been going on. Now one could
compare the ball flying off with the ball still attached to the string.

The one still attached to the string would continue uniformly in a circle. By comparing the position of the released ball with that of the circling one, he showed that, at least for a short time, the difference between the two positions was exactly what Galileo had found for a dropped ball-- ie the distance between the free ball and the circling ball obeyed the Merton rule. In successive equal time intervals the ball was 1 unit, 4 units, 9 units, 16 units... away. The distance increased as the square of the time. It would seem, at least for that a while, that the ball attached to the wheel would behave with respect to the released ball, as if it were constantly accelerated toward the wheel. If one waits (eg in the last pair of positions in the diagram) there is also a displacement in the dirction of the motion, but this is small and goes rapidly to zero for the ones closer to the release point right at the top. This constant acceleration was proportional to the speed squared of the ball in its circling, and inversely proportional to the radius of the wheel. (For a larger string whose ball moves at the same velocity, the divergence between the straight motion and the circular motion in the same time is less. The object on the string is "falling" away from the straight line less rapidly). The force is thus proportional to the inverse radius of the string. Thus, you, holding the rope swinging the object around, must be supplying the force causing the object to go in a circle (falling away from the straight line motion). That force would clearly also be proportional to the mass of the object-- swinging a larger mass around your head at the same speed you have to pull harder on the rope to keep it from flying away.
Circular motion requires some sort of force to keep the object moving in that circle. Of course these experiments are all being done on scales much smaller than the size of the earth, so there is not way to distinguish Galileo's circles around the earth as "natural motion" from staight lines as "natual motion". But clearly the situation was becoming ripe for the next advance which was Newton.
Huygens even applied this argument to the earth and the question of the earth's spinning. One argument against the earth's spinning was that, like mud on a wagon wheel spinning rapidly, we would be flung off the surface of the earth by its spinning. After all if the 6400 km radious earth was to revolve once per day, it would have to have the stupendous velocity of more than 1600km/hr. Surely that would fling away everything. But Huygens knew that what was important was not just the velocity, but also the radius of the earth, since the force (or the acceleration) is proportional to the inverse of the radius, and the earth is large. Dividing 1600 km per hour squared = (250 meters per second) by 6.400 million meters gives about 1/100 meters per (second squared) as the acceleration neeed to hold something down onto the surface of the earth. But Galileo had shown that the acceleration of down of things on the surface of the earth was about 10 meters/second square. -- ie, Galileo's acceleration was about 1000 times greater than was needed to hold things down if the earth were rotating. Centrifugal force was not an impediment to the earth's rotating.
There was a consequence of this as Newton recognized.-- the downward force of gravity at the poles (where there was no centrifugal force) would be greater than at the equator. Thus the stuff of the earth would tend to get pulled in more at the poles than at the equator, making the earth bulge slightly at the equator. The distance around the earth at the equator should be very slightly larger than the distane around the earth through the poles. If you go to Google Earth, you find that this is true, and the circumference at the equator is about 65 km larger than the circumference through the poles. (The radius from the center to the poles is about 22 km less than the distance from the center to the equator). When these were measured in the 18th century, it provided one of the first experimental demonstration that the earth did rotate. Mind you no-one doubted it by then, but it would have been really embarassing if the measurements had not agreed with Newton's argument.
Thus by the late 1600, one had some principles which seemed to be clear. One was that the the "natural motion" of objects was in straight lines, not in the horizontal circles around the earth that Galileo discussed. The second was that in collisions, the center off mass should keep moving uniformly. The third was that in order to keep an object moving in a circle, one needed a force acting on the object, a force proportional to the mass, inversely proportional to the radius of the circle, and directly proportional to the distance. That force was the directly palpable effort that one needed to put into keeping the object travelling in a circle.
One aspect of the these forces was that they had to be transmitted by some material from one thing to another. It filled both Descarte and Huygens with revulsion to think of forces in the absence of an agent to transmit that force (eg the string, or the spokes of the wagon wheel, if one were interested in the the ability of mud to cling to the wheel, etc).
The radius of the earth is about 6400 km, or 6.4 million meters. The circumference of the earth at the equator is then 2 pi 6.4million m= 40million meters. One day is 86400 seconds, so the speed of rotation at the equator is 40million m/86400 sec = 465 m/sec. The centrifugal acceleration is thus 465squared /6.4 million = .033 meters/second squared =1/30 m/sec^2

Galileo showed that the acceleration at the surface of the earth was about 10 meters /sec squared, which is 300 times larger than the acceleration needed to keep objects held to the earth. Ie, things being flung off the earth is not an argument against the rotation of the earth.
Note that Newton used this to argue that there was a way to determine that the earth actually rotated. Since things on the equator are flung out slightly one would expect the radius of the eath at the equator to be slightly larger than it is at the poles, where there is not "outward flinging". It is. The radius at the poles is about 22 km less than the radius at the equator. This was measured about a hundred years after Newton. It is a difficult experiment since one had to measure distances on the earth to better than about .1%.
copyright W Unruh (2018)